As a side project right now I’m investigating computer languages — not just experimenting with Perl vs. Python but trying to expose myself to different families of languages, such as functional, logic, imperative, object oriented, and obfuscated.
Most recently, someone mentioned that array languages are the least
widely known family — perhaps because the founding language in the group,
APL, was written with a nonstandard character set. Perhaps the most terse
of all programming languages, APL spawned a series of children, like J and K,
which, even though they can be written in a normal alphabet, retain APL’s
essential terseness — or, dare we say, obscurity?
I plan to learn J. However, before I did so, I committed myself to learning
at least a smidgen of the original APL, so I could see how the language was
originally intended to work and look.
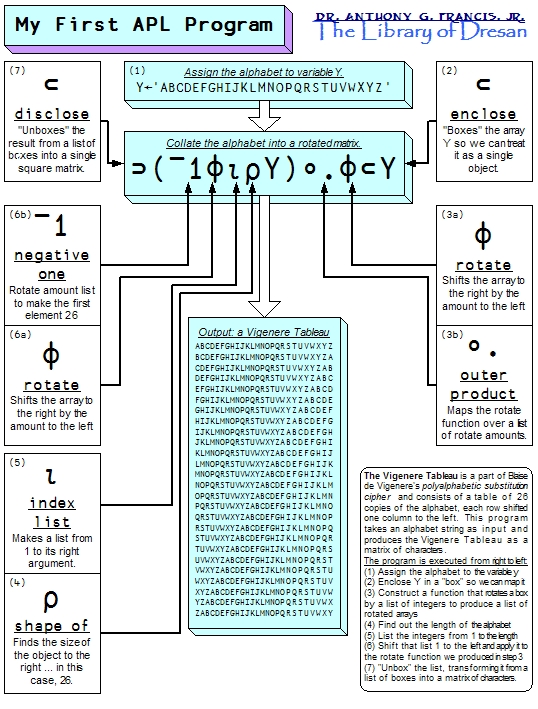
Here’s my first APL program, designed to produce a Vigenere tableau:
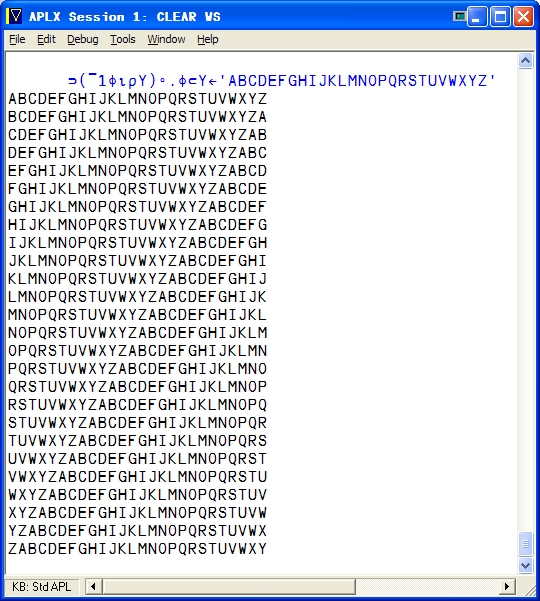
Note the code isn’t in the standard ASCII character set, so I had
to represent it as an image file.
The heart of the code is the central box of the next image. This should read as:
disclose (( -1 rotate (indexList (shapeOf Y)))
(outerProduct rotate) (enclose Y))
and executes right to left:
To translate into pseudocode:
// Assign the alphabet to the variable Y
Y = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
// Now perform the following:
(unbox
((outerproduct rotate)
(rotate -1 (enumerate (length y)))
(box y)
)
)
// This is the moral equivalent of:
// (1). Treat array Y like a "scalar" variable
boxedY = box(y)
// (2) Find the length of Y - in this case,26
lengthOfY = length(y)
// (3) Get an array from 1 to the length of Y
// We will use this (1 2 ... 26) later to
// rotate the alphabet to the side
list1toY = enumerate(lengthOfY)
// (4) Rotate list by one so that the first
// row is a "no-op" rotation: (26 1 2 ... 25)
// (I should have just have subtracted one
// from each list to get (0 1 .. 25), but
// it's just my first APL program!)
rotateAmounts = rotate(-1, list1toY)
// (5) Create a "mapping rotate" function that takes
// a list of integers as its first argument and
// rotates each element of its second argument
// by the supplied integer.
// We had to "box" Y earlier because APL by
// default treat each of its elements as a one-element
// array.
mapRotate = outerproduct(rotate)
// Now create 26 copies of Y, each rotated by the amount
// specified in the rotateAmounts variable, and collect
// them all into a list. This is morally equivalent to:
// list(
// rotate(26, boxedY),
// rotate( 1, boxedY),
// ...
// rotate(25, boxedY)
// )
rotatedY = mapRotate(rotateAmounts, boxedY)
// Now "unbox" the rotated list, which takes the
// list of lists of rotated Ys and turns them into
// a matrix or grid rotation
return unbox(rotatedY)
The idea in my mind was to take an input array and print
a diagonalized rectangle with it. With the alphabet, this
becomes a Vigenere table — once the “indecipherable cipher”,
now a trivial matter for any modern computer.
With a different string, like “01” or “_[]” (reading the two
brackets as the APL Quad character), and a suitable change
in length of the output, it becomes instead a checkerboard:
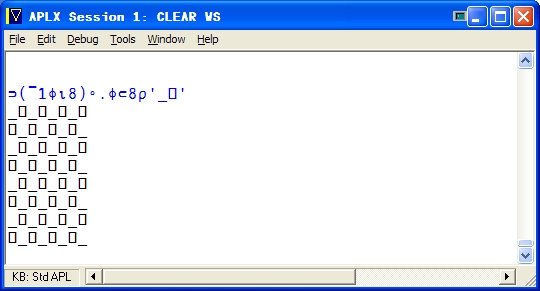
Deciphering that is left as an exercise to you, dear fanu.